累乗根の [1/1] パデ近似

はじめに

点 $x=x_0$ の周りにおける 関数 $f\left(x\right)$ の $[m/n]$ パデ近似とは， 有理関数 $f_{m/n}\left(x\right)=P\left(x\right)/Q\left(x\right)$ （ただし $P\left(x\right)$, $Q\left(x\right)$ はそれぞれ $m$, $n$ 次多項式）であって， $x=x_0$ の周りにおけるテイラー展開の係数が 元の関数 $f\left(x\right)$ と $m+n$ 次まで一致するもののことである[BG, p. 1]．

累乗根の [1/1] パデ近似は覚えやすい形をしており，計算精度も高い． この記事では， $x=1$ の周りにおける $n$ 乗根関数の [1/1] パデ近似の式を導く． また，応用例として $\sqrt{47}$, $\sqrt[3]{42}$ の近似値を計算する*1．

導出

[1/1] パデ近似なので， 分母・分子が共に1次の有理関数であって， そのテイラー展開が累乗根のテイラー展開と2次の項まで一致するものを求めたい． はじめに，関数 $f\left(x\right)=\sqrt[n]{x}$ を $x=1$ の周りで展開する． $x=1+\epsilon$ とおくと， $$\sqrt[n]{x}=1+\frac{1}{n}\epsilon -\frac{n-1}{2n^2}{\epsilon }^2+\cdots$$ である． 次に， $f_{\mathrm{1/1}}\left(x\right)=(ax+b)/(cx+d)$ を $x=1$ の周りで展開する． 先ほどと同様に $x=1+\epsilon$ とおくと，次のようになる． $$\frac{ax+b}{cx+d}=\frac{a+b}{c+d}+\frac{ad-bc}{{(c+d)}^2}\epsilon -\frac{c(ad-bc)}{{(c+d)}^3}{\epsilon }^2+\cdots$$

$f\left(x\right)$ と $f_{\mathrm{1/1}}\left(x\right)$ のテイラー展開が2次の係数まで一致すると仮定すると次の式を得る． $$\frac{a+b}{c+d}=1,\frac{ad-bc}{{(c+d)}^2}=\frac{1}{n},\frac{c(ad-bc)}{{(c+d)}^3}=\frac{n-1}{2n^2}$$ この連立方程式を解く． 未知変数は $a,b,c,d$ の4つであるが，条件が3つなので自由度が1つ余る． ただし，この自由度は分母と分子を定数倍するだけなので，関数 $f_{\mathrm{1/1}}\left(x\right)$ は結局1つに定まる．

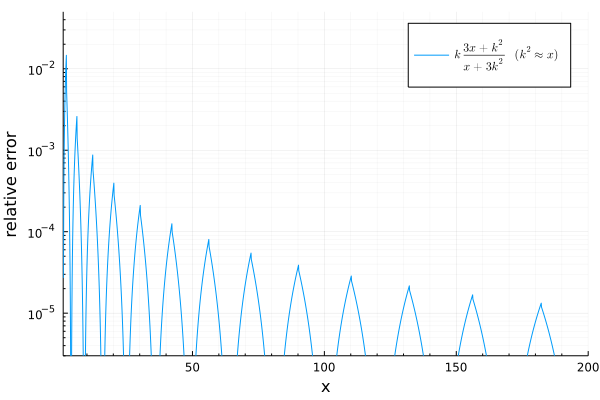
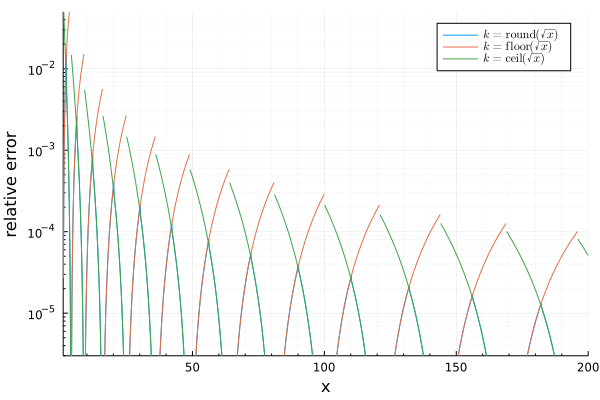
まず， $c/(c+d)=(n-1)/2n$ より $c=n-1$, $d=n+1$ としてよい． これを代入すると $$a+b=2n,(n+1)a-(n-1)b=4n$$ を得る． ここから $a=n+1$, $b=n-1$ が分かる． 以上より $$f\left(x\right)\approx f_{\mathrm{1/1}}\left(x\right)=\frac{(n+1)x+(n-1)}{(n-1)x+(n+1)}$$ となる． $x$ を $x/t$ で置き換えると，最終的に次の式を得る． $$\sqrt[n]{\frac{x}{t}}\approx \frac{(n+1)x+(n-1)t}{(n-1)x+(n+1)t}$$ たとえば， $n=3$ のときは次のようになる． $$\sqrt[3]{\frac{x}{t}}\approx \frac{4x+2t}{2x+4t}=\frac{2x+t}{x+2t}$$

係数の順番がややこしいが， $x=0$ を代入したときに誤差が小さくなる方と覚えておくと忘れにくい．

計算例

例1． 47 の平方根を考える． $t=49$ とおくと次の近似値を得る． $$\sqrt{47}=7\times \sqrt{\frac{47}{49}}\approx 7\times \frac{3\times 47+49}{47+3\times 49}=\frac{665}{97}=\mathrm{6.855670\cdots }$$ $${\left(\frac{665}{97}\right)}^2=\mathrm{47.00021\cdots }$$ 実際には $\sqrt{47}=\mathrm{6.85565460\cdots }$ （相対誤差 2.3 ppm）である．

例2． 42の立方根を考える． $t=27$ とおくと 次の近似値を得る． $$\sqrt[3]{42}=3\times \sqrt[3]{\frac{42}{27}}\approx 3\times \frac{2\times 42+27}{42+2\times 27}=\frac{111}{32}=3.46875$$ $${\left(\frac{111}{32}\right)}^3=\mathrm{41.73678\cdots }$$ 実際には $\sqrt[3]{42}=\mathrm{3.4760266\cdots }$ （相対誤差 0.21 %）である． 精度を上げるため， $111/32$ に近い簡単な分数として適当に $7/2$ を取ってもう一度計算すると $$\sqrt[3]{42}=\frac{7}{2}\times \sqrt[3]{\frac{42\times 2^3}{7^3}}\approx \frac{7}{2}\times \frac{2\times 42\times 8+343}{42\times 8+2\times 343}=\frac{16\times 42+343}{2\times (48+98)}=\frac{1015}{292}=\mathrm{3.476027397\cdots }$$ $${\left(\frac{1015}{292}\right)}^3=\mathrm{42.00002727\cdots }$$ を得る（相対誤差 0.22 ppm）．

追記１：ハレイの方法について

(2024-01-09 作成)

この記事について愛知県の林邦英さんからお手紙 (2023.11.29) が届いた． 大変ありがたいことです． 林さんについて調べてみると，連分数論や近似論について精力的に研究なさっているようで， 沢山の研究資料がオンラインで公開されている *2． その中でも資料 [H] によると， 平方根の近似式 $$\sqrt{x}\approx \frac{3x+1}{x+3}$$ にはハレイの方法という名前がついているらしい． これは知らなかった． 博論の提出が終わったらハレイの方法についてもう少し調べたい……．

林さんからのお手紙には，常用対数の計算手法に関する結果もまとめられていた． しかしまだきちんと読めていない……大変申し訳ないことです． 内容をちゃんと理解できたら別記事とお返事のお手紙を出したい．

更新履歴

• 2022-09-14: 公開
• 2023-04-02: Document ID を追加
• 2023-12-03: 名前を間違えていたので訂正
• 2024-01-09: 追記１（林さんからのコメントを受けて）

Permanent ID of this document: 4a465cdb12bc8608219aff4fd20e7b4a

脚注

参考文献